Just began working through Programming Pearls by Jon Bentley. So far, it’s fun with really engaging problems and solutions. Like this one:
Rotate a one-dimensional array of N elements left by l positions. For instance, with N=8 and l=3, the vector ABCDEFGH is rotated to DEFGHABC. Simple code uses an N-element intermediate vector to do the job in N steps. Can you rotate the vector in time proportional; to N using only a few extra words of storage?
The ’naive’ solution provided is well, naive. And as the problem prompts, we can do better.
The first solution that popped up in my mind was linked-lists - linked-lists just seemed like the kind of data-structure meant for rotations: if the array could somehow be converted into a linked-list, followed up by traversing the first l elements and juggling a couple of pointers, the problem could be solved. But this seemed to have more overhead and would have ended up taking more space than simply allocating an intermediate n-element array and using it for the rotation. Besides, as Bentley pointed out later on from Kernighan’s report, folks who based their solution on linked-lists concluded that such an approach tends to be bug-ridden.
While trying to work something else out, it hit me that all array rotations are merely a subset of permutations. Formally, from Artin’s Algebra book, a permutation of a set S is a bijective map p from the set S to itself. That’s quite a mouthful. Think of permutations as just a different orderings or arrangements of the same elements. Again, formally, the cycle notation is used to represent permutations. To illustrate how this notation is derived, consider the diagram below:
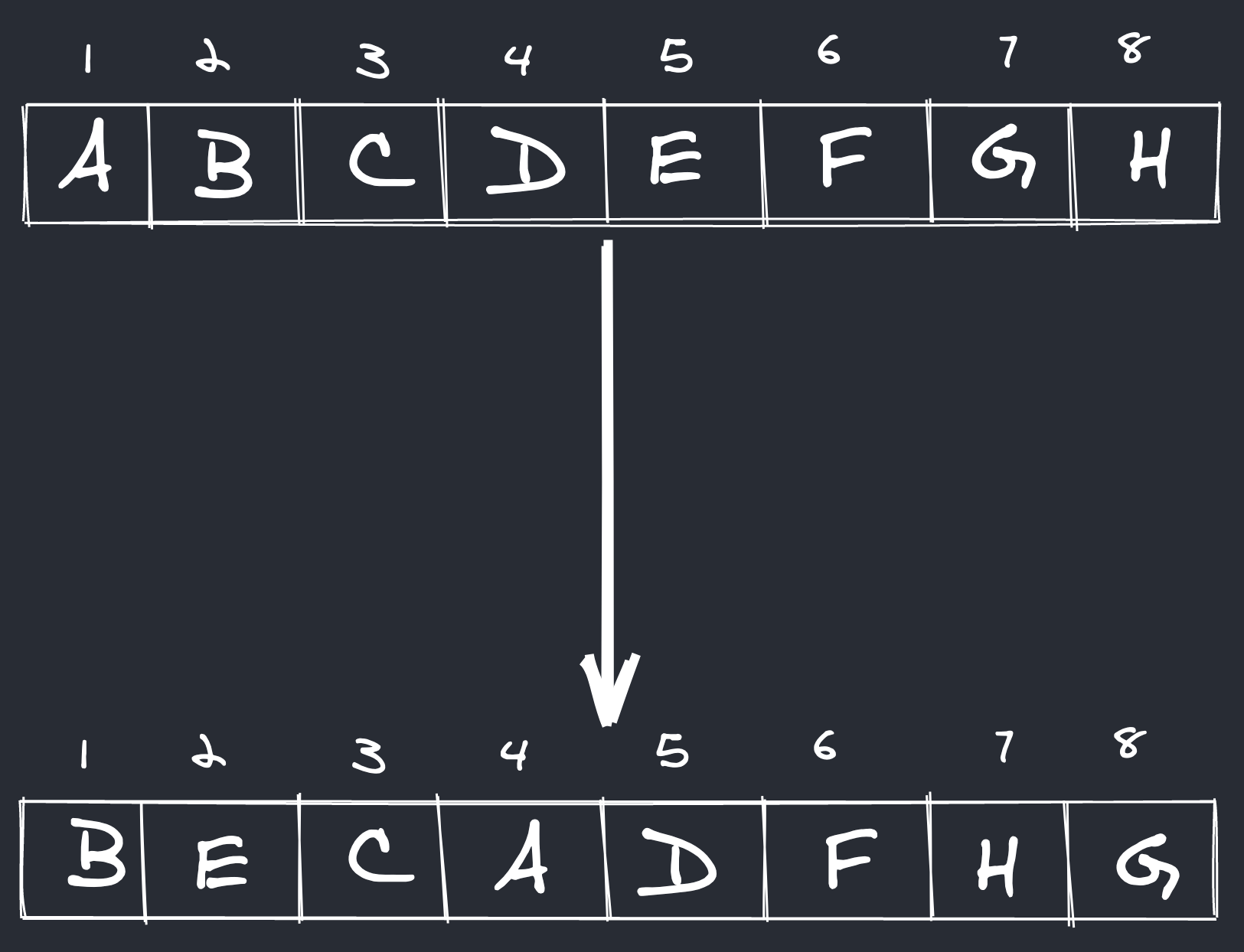
a’s index moves from 1 to 4. The element that was in the 4th index, d, has its index move from 4 to 5. As for e, 5 to 2 and b, 2 back to 1, a’s index. A cycle! This can be represented as (1452). c and f remain in the same position. g and h are swapped, forming another 2-cycle (78). The whole permutation can be represented as (1452)(78). The 1-cycles for c and f are usually omitted from the representation. Do note that the cycle notation representation of a permutation is not unique, for example, (341), (134) and (413) both represent the same permutation.
Now back to array rotation, if you work it out, the rotation ABCDEFGH → DEFGHABC in cycle notation form is (16385274). With this, it becomes trivial to rotate an array: just allocate extra space for a single element and use it to swap around the elements till the end of the cycle. Now, all that remained was to find a way to generate the cycle representation of a given a rotation efficiently.
Pencil to paper and a couple of minutes later on, this is what I had: if moving an index to the left by 3 is like substracting but I still want the index to be within the range [1,8] then I have to use modulo somehow. This totals up as: to get the ith element’s next position, calculate (i - 3) mod 8. For example (1 - 3) mod 8 = 6 and (6 - 3) mod 8 = 3 and so on and so forth.
Bringing in everything together in Python, we have:
def rotate(arr, steps):
temp, i, N = arr[0], 0, len(arr)
for _ in range(N):
i = (i - steps) % N
arr[i], temp = temp, arr[i]
arr = list("ABCDEFGH")
rotate(arr, 3) # DEFGHABC
Satisfied with my solution, I decided to compare it with Bentley’s, hoping that we both arrived at the same solution.
Aaand… what can I say, his was more profound - and true to the chapter’s title, a definite Aha! algorithm.
The first insight that Bentley provides is that if we partition the array into AB where A has first l elements and B has the rest, then rotation boils down to transforming AB to BA.
From there, let the superscript r denote either the operation of reversing elements within an array or reversing the order of partitions.
As the image below shows, to rotate the array, we first reverse the elements within the first partition and the second partition: A→A^r, B→B^r.
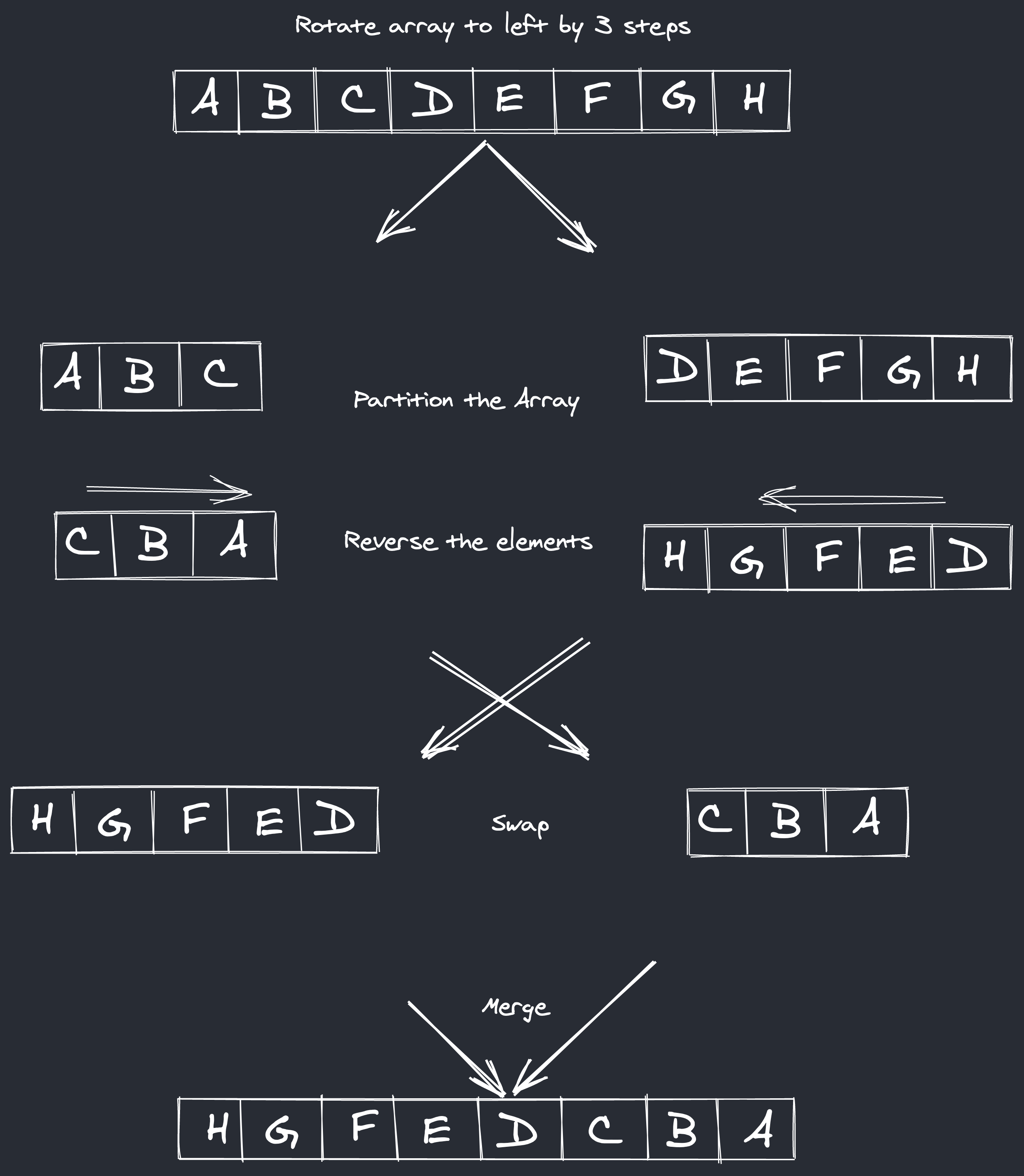
From there, we swap both partitions, resulting in (A^rB^r)^r, which ends up as… BA, exactly what we wanted.
Problem solved!