Generalized Range Difference, Recursion & Search Availability in PostgreSQL

Amongst the interesting data-types offered in Postgres are the Range Types, such as the daterange and int4range. If you haven’t encountered them yet, Postgres' own documentation is a great place to start. Postgres also offers range-specific functions and operators that enrich the use of ranges. One of these operators is the difference operator, ‘-’ which uses the minus symbol and is better demonstrated with sql code:

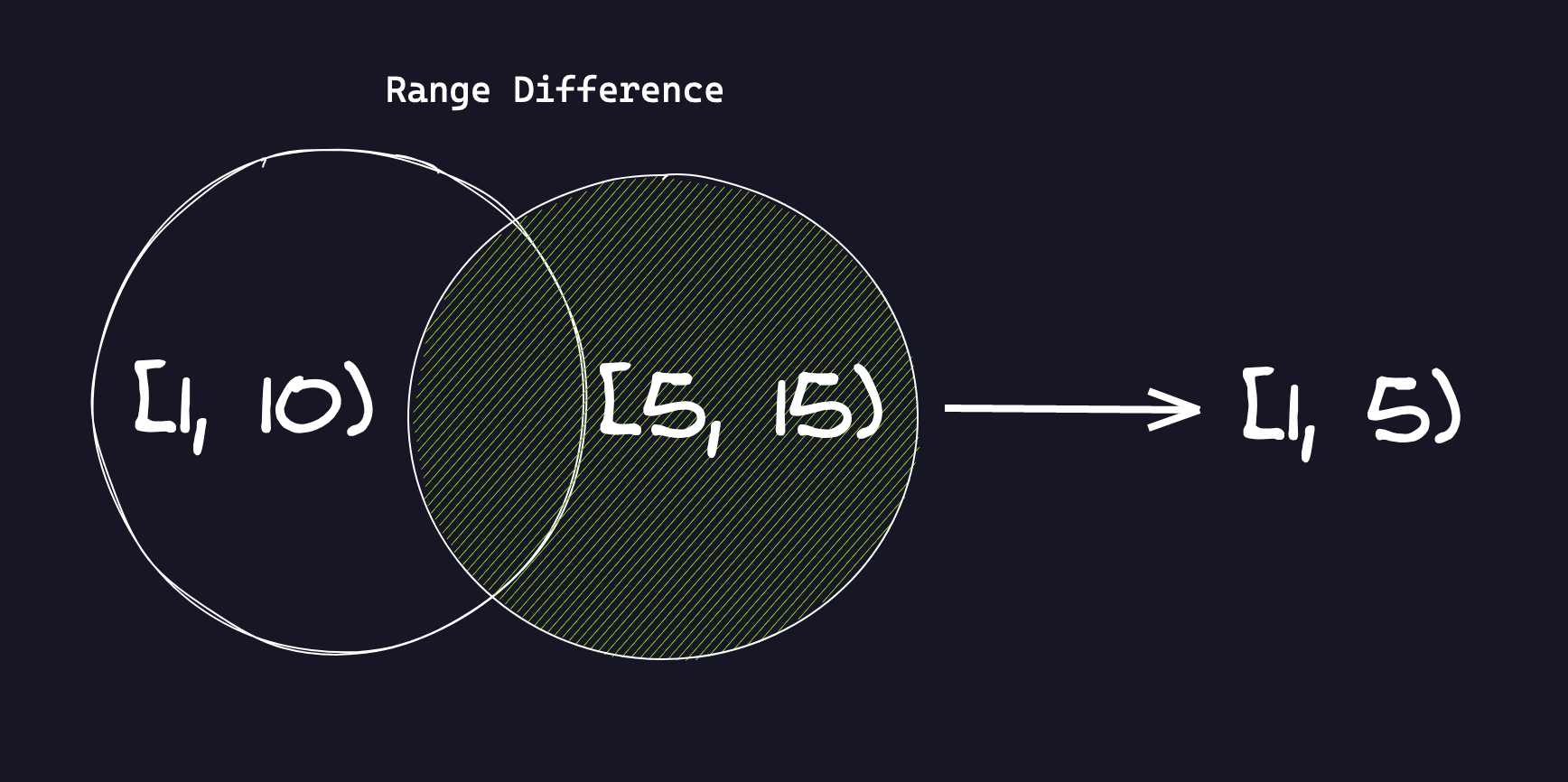
select int4range(1, 10) - int4range(5, 15);
-- [1,5)

If we think of the int4ranges as sets in the mathematical sense, int4range(1, 10) represents the set of all integers greater than or equal to 1 but less than 10. By default the lower bound is inclusive and the upper bound is exclusive. The same’s the case with int4range(5, 15). Therefore, the difference operation above results in a range consisting of all integers that are in the first range but are not elements of the second range, hence [1,5) - the set difference.

For most of the cases, range difference operates pretty much as one would expect of set differences, even when both ranges are entirely disjoint. However, if the second operand is fully contained within the first operand, the range difference fails.

select 
    int4range(1, 100) - int4range(10, 20); -- ❌
--  ERROR: 22000: result of range difference would not be contiguous
-- LOCATION:  range_minus, rangetypes.c:993

This makes sense since, as the error message indicates, we end up with disjoint sets. Without such a restriction, the return value would have been [1,10), [20,100) but then, the column in the resulting table would have to accomodate more than 1 value at a go, breaking the relational model.

Still, a generalized range difference (that handles all cases) is useful for various applications. One chief example is on search availability, as detailed in Jonathan Katz’s blog post for Crunchy Data. In a nutshell, given a set of date/time ranges that indicate when an item or a room or a schedule is booked, find all the freely available slots within a given range i.e. the ‘gaps’. I’d suggest you go through Katz’s post first if you have a couple of minutes to spare. Specifically, you should check out the sql implementation of his solution for the search availability problem - it took me a while to wrap my head around the travels_get_available_dates function in the post but it was well worth it given its ingenuity. However, when I transcribed the code and ran it on a couple of values, the function kept erroring out on date ranges that were directly adjacent to each other. This could entirely be attributed to coding errors on my part but overally, it prompted me to try working out a different approach that’s able to handle such edge cases correctly all while maintaining efficiency. Hence this post.

Before getting to my approach for search availability, I’d like to point out that another reader also encountered the same error (regarding adjacent dates) and posted it on stack-overflow - link. I haven’t tried out other folks’ solutions from the comments yet but I did add mine plus a more in-depth description on how (I think) the error in the travels_get_available_dates function arises - link.

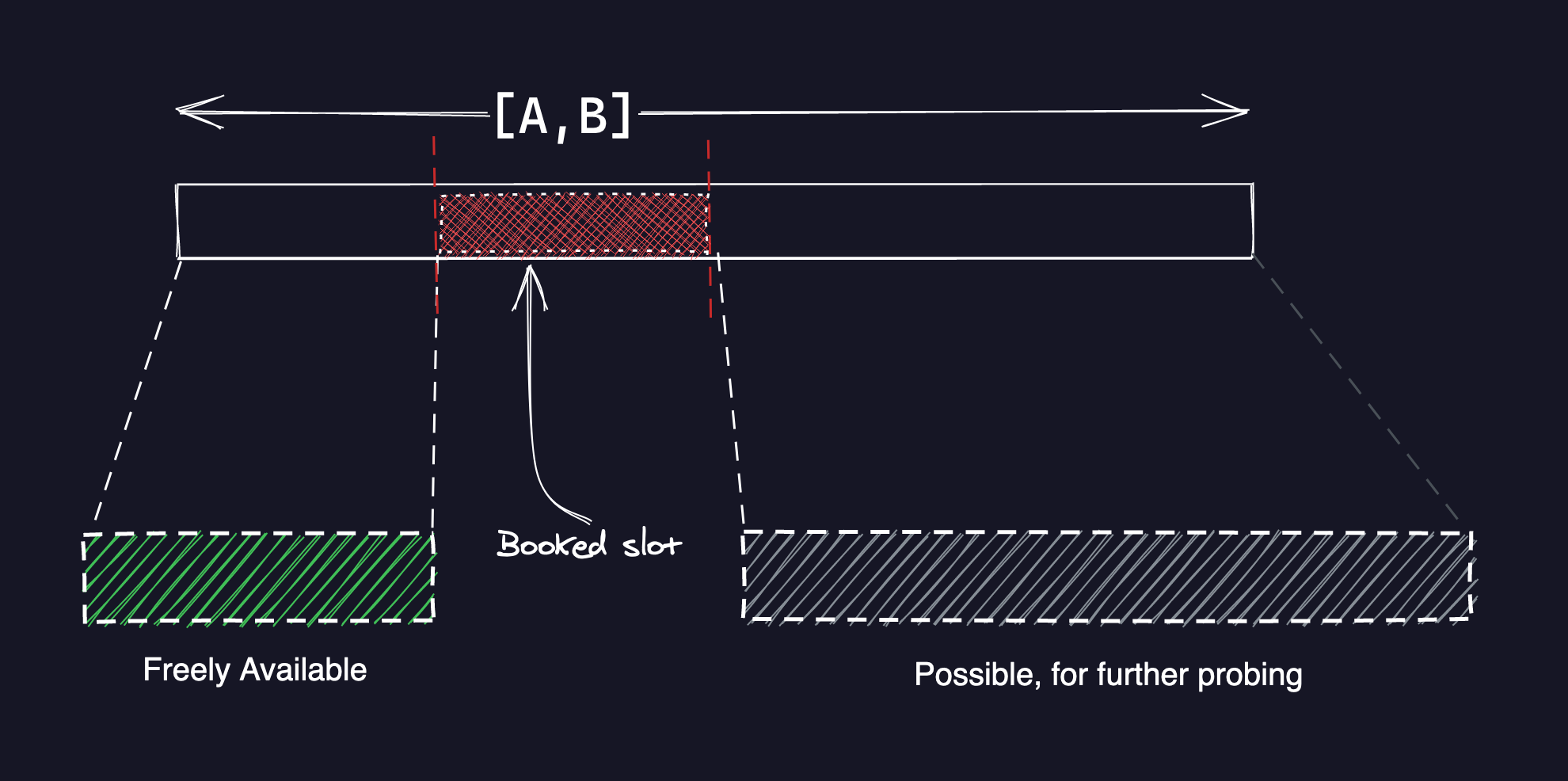
Okay, here’s an overview of my approach. Given a range [A,B] we want to find all the freely available slots.

1. First, narrow down exclusively to booked slots, that overlap or intersect with the search range [A,B].
2. Sort the booked slots from the smallest to the largest
3. From there, iterate over the booked slots in ascending order
4. With each iteration, the booked slot divides [A,B] into two sections, the freely available chunk, which is in the left, and the remainder chunk for further probing as shown in the diagram below
5. Gather up all the freely available chunks and on completion, we end up with all the freely available chunks!

Now, the next hurdle is translating the logic to SQL, which was a bit hard for me at first since it’s imperative (and as we all know, SQL is declarative). Moreover, I had the inkling that it might end up being quite inefficient, but we’ll get to that part later on. Like Katz, my approach relies on recursive CTEs. As a side-note, even though SQL uses the keyword with recursive, I’ve always found it easier to think of recursive CTEs as iteration just as the Postgres documents suggest: we start with the base case as the result table and for each ‘iteration’, we build a working table which is ‘appended’ to the result table. Iteration stops once the working table is empty i.e there’s nothing more to add to the final result table.

For the sake of tinkering and debugging, I shifted from dateranges to int4ranges since they are much easier to read and inspect. The demo table I used is defined as follows:

create table bookings(
    id serial primary key,
    slot int4range not null default 'empty'::int4range,
    exclude using gist (slot with &&)
);

From there, I inserted 1 million random ranges using a really inneficient Go script which I won’t post to avoid further embarrassment. And Without further ado, here’s the SQL code for finding all the available slots within the range [1, 100000):

with recursive selections(available, possible) as (
    select 'empty'::int4range, int4range(1,100000)
union
    select
        case 
            when already_booked is null 
                then possible
            when possible @> lower(booked) 
                then int4range(lower(possible), lower(booked))
            else 'empty'::int4range
        end as available,
        case when possible @> upper(booked) 
                then int4range(upper(booked), upper(possible))
            else 'empty'::int4range
        end as possible
    from selections
    left outer join lateral ( 
        select slot as booked from bookings
        where slot && selections.possible
        order by slot asc limit 1
    ) as already_booked on 't'
)
select available
from selections
where not isempty(available)

The non-recursive term, copied below, is straighforward, we start with a single row consisting of two columns, available and possible. The value on the available column is an ’empty’ range since so far we haven’t extracted a single free slot; the value on the possible column is the entire range within which we want to get all the available slots, int4range(1,100000).

with recursive selections(available, possible) as (
    select 'empty'::int4range, int4range(1,100000)

To get the first available slot, we first retrieve the lowest range that intersects with the possible range (which starts as [1, 100000)) and pair it up with the current row in the working table (there’ll always be a single row in the working table). This is carried out in the join clause:

-- ...
from selections
left outer join lateral ( 
    select slot as booked from bookings
    where slot && selections.possible
    order by slot asc limit 1
) as already_booked on 't'
-- ...

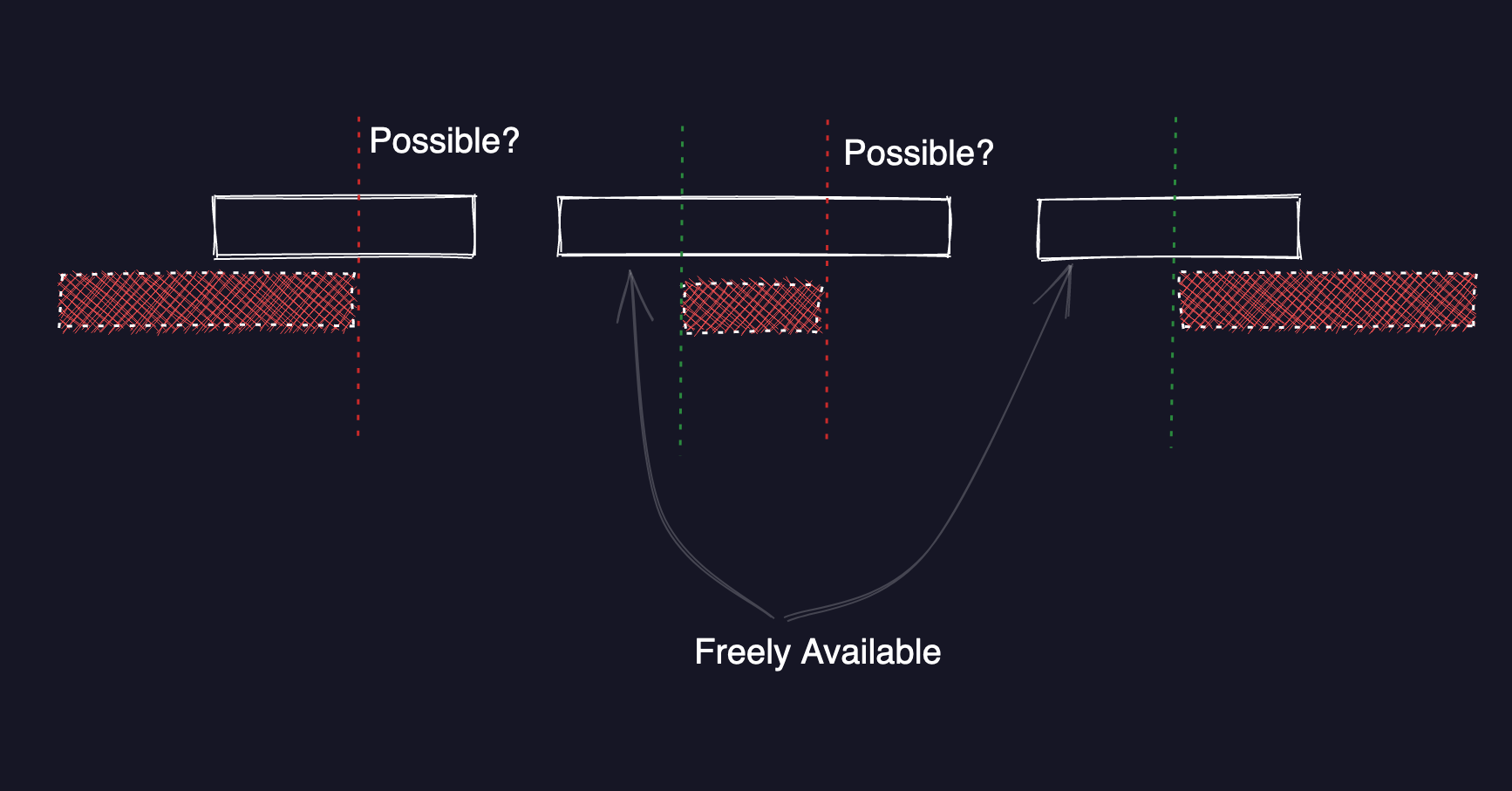
From there, the already_booked range value is used to split up the possible range into two, the available and the remainder which serves as possible in the next ‘iteration’. The case ... when clauses handle different edge cases such as when the already_booked range is entirely within the possible range or it extends further to the left or further to the right, as shown in the diagram below:

Finally, let’s talk about termination. There are two possible approaches that I had in mind:

1. use where clause for the working table to determine when there are no more slots to consider
2. use the union clause…

As you’ve seen in the code-sample above, I opted for the second option. It works out as follows: at some point, when there are no more bookings to probe, the row returned from the iterative step will be ('empty', 'empty'). On the next iteration, the row returned will be ('empty', 'empty') again. Now, since union in this case discards duplicates, it will discard the second ('empty', 'empty') and the working table will be empty, at which point the iteration/recursion will halt.

I arrived at this option entirely by accident since I forgot to add the where clause, but somehow it kept on working. When I noticed it, at first I thought it was a bug that might result in an infinite loop given the following scenario: the SQL engine decides to pluck out the duplicate from the final table rather than the working table which then remains non-empty. If this is done over and over again, well, we end up with the infinite loop. However, Postgres’ documentation does seem to guarantee that the duplicate row will be plucked out from the working table rather than the result table - link:

… Evaluate the recursive term, substituting the current contents of the working table for the recursive self-reference. For UNION (but not UNION ALL), discard duplicate rows and rows that duplicate any previous result row…

Still, for the sake of clarity, I opted for the where clause to make the termination condition explicit. All in all, for reusability, I wrapped it into an SQL function. I also shifted to union all since as long as booked slots don’t overlap, there shouldn’t be any non-empty duplicate rows in the result to begin with.

create or replace function get_available(int4range)
returns table(available int4range)
as $$

with recursive selections(available, possible) as (
    select 'empty'::int4range, $1
union all
    select
        case 
            when already_booked is null 
                then possible
            when possible @> lower(booked) 
                then int4range(lower(possible), lower(booked))
            else 'empty'::int4range
        end as available,
        case when possible @> upper(booked) 
                then int4range(upper(booked), upper(possible))
            else 'empty'::int4range
        end as possible
    from selections
    left outer join lateral ( 
        select slot as booked from bookings
        where slot && selections.possible
        order by slot asc limit 1
    ) as already_booked on 't'
    where not isempty(possible)
)
select 
    available
from selections
where not isempty(available)

$$ language sql stable;

Now, for the moment of truth, how does it measure up against Katz’s solution. In terms of ease of understanding, it’s definitely simpler. However, what should matter more is its efficiency. Before comparing both, my assumption was that Katz’s approach should take the cake since it operates with a larger working table during each recursive step, hence narrows down the options much faster, whereas mine works with a single row at a go. For the test data, all the slots were non-overlapping and non-adjacent. Given 4 booked slots, my approach took 2.057 ms whereas Katz’s took 4.633 ms to return all the available slots. Now, this is where things get interesting - given 18 booked slots, mine took 3.584 ms vs. 3392.68 ms! At 42 slots, it ends up as 10.454 ms vs. ∞. And with 2,284 slots its 5689.236 ms vs. ∞ ^ ∞. Just kidding on the infinity part, but I had to cancel Katz’s query since it was taking too long. Now, there are a lot of factors skewing the results, the chief one being, my laptop’s hard disk is almost full and I should probably move stuff out to elsewhere. But I’m glad that my approach wasn’t relatively as slow as I’d earlier presumed. So if you’re interested, you can definitely try to benchmark both versions and see what works best for you! All comments, suggestions and corrections are welcome.